・ function setting
探索対象の関数を設定します。
- [<x<]、[<y<]
- 関数の定義域を入力します。
- [function]
- 関数を入力します。入力形式は、c言語やjavaにおける識別子に似せてあります。
- 変数:x, y
- 定数:PI, E
- 四則演算:+, -, *, /
- javaで使える関数:sin, exp, log, pow, abs, sqrt,random
等
- 条件式:==, !=, <, >, <=, >=, ||, &&
,!
- 条件分岐:if (条件式) 式1 else 式2
- 入力例:sin(x)+cos(x-y)+1/(exp(x*x+y*y)+pow(x,4)+1.5)
- [choice]
- あらかじめ設定されている関数を選択します。
- DeJong F1〜F5は、GAのベンチマークテストや他の手法との定量的評価手段として用いられる標準関数です。
- 以下にその定義を示します。
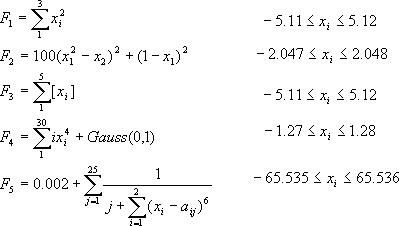
- これらは最小値を求めるものですが、このアプレットでは符号を反転して最大値を求める問題に置き換えています。またDeJongF1,F3,F4は3変数以上の問題ですが、2変数の問題になるように式を簡略化しました。
・ viewer settings
右上の関数ビューへの表示の設定をします。
- [color scale]
- 関数の配色の設定をします。関数値が大きくなるにしたがって、グラフの色が青から赤に変わります。その変わりはじめと終わりの関数値を指定します。
- [z scale]
- 関数値とパラメータのx,yとの表示の際のスケールの比を設定します。たとえば2を入力すると、グラフの高さが2倍になります。
・ search method settings
探索手法の設定をします。
- [search method]
- 探索手法を選択します。
- GA
遺伝的アルゴリズム(Genetic Algorithm)です。遺伝的アルゴリズムとは、生物の進化にヒントを得た最適化を高速に行う探索アルゴリズムの一種です。遺伝子をもつ仮想的な生物の集団を突然変異や交叉により進化させます。その際、より環境に適したもの(より適合度が高いもの)を生き残りやすくします。
関数ビューに表示される点が集団をあらわしています。各個体の座標と遺伝子が一対一に対応しています。各個体の適合度は、その点における関数値です。個体の適合度が高くなるにつれ、個体の色は緑から黄色に変化します。
- SAHC,NAHC,RMHC
これらはすべて山登り法(Hill Climbing)の一種です。山登り法とは、その時目の前にあるもののうち一番良いものを選びつづけるアルゴリズムです。ビューに表示される緑の点が、登山中の個体を表しています。個体はGAの場合と同様に座標に対応した遺伝子を持ちます。SAHC,NAHCは、これ以上関数値の上昇が望めない位置に到達すれば、ランダムな位置から再び探索を開始します。その際見つかった頂点は黄色の点で表示されます。
- [max generation]
- 最大の世代数。
- [population size]
- 集団の個体数。
- [evalutation time]
- 山登り法において、探索終了までの関数の評価回数。GAの場合の関数評価回数は[max generation]*[population
size]です。
- [crossover probability]
- 選ばれた2個体が交叉する確率。
- [mutaion probability]
- 遺伝子座(遺伝子の各ビット)一つあたりの突然変異が起きる確率。
- [gene length]
- 遺伝子長(遺伝子のビット数)。
- [generation gap]
- GAオペレータ(突然変異、交叉)が適用されずにそのまま次世代にコピーされる個体の数。
- [number of elite]
- エリート戦略で次世代に残す優良個体の数。適合度の高いものから順に残されます。エリート数は世代間のギャップに含まれるため、[number
of elite]は[generation gap]以下でなければいけません。
- [coding method]
- 個体の座標をビット配列である遺伝子に写像する際のコーディングの手法。バイナリコーディングは座標の10進数表記を単純に2進数表記に変換するだけの方法です。一方グレイコーディングは、隣り合った座標のハミング距離(遺伝子間の異なる遺伝子座の数)が1となるように、バイナリコーディングの2進表記を変換する方法です。
- [selection method]
- 個体の選択方法。ここで選択された個体がGAオペレータによる操作を経て、次世代の集団を形成します。
- tournament
トーナメント方式。集団からある個体数(トーナメントサイズ)分ランダムに選び出して、その中で一番良いものを選択します。この過程を集団数が得られるまで繰り返します。
- roulette
ルーレット方式。適合度に比例した領域を持つルーレットを回し、ルーレットの玉が入った領域の個体を選び出します。この方法で集団数分を選び出します。適合度は負になる場合もあるので、シグマスケーリングにより変換された適合度を用いてます。
- [tournament size]
- 上記のトーナメント法におけるトーナメントのサイズ。
- [sigma share]
- 近親度(sharing)を求める関数のパラメータ。遺伝子が近い個体が多い個体ほど適合度が小さくなるようにして、集団の多様性を維持したいときに設定します。この値が0のときは近親度を考慮しません。
- [crossover method]
- 実数値GAで用いる交叉方法を選択します。
- BLX-α
両親の遺伝子が表す実数値ベクトルの区間を両方向にαだけ拡張した区間から、一様乱数に従ってランダムに子を生成する手法。
- UNDX
2個体の親を結ぶ直線の周辺に正規分布に従って子を生成する手法。このとき第3番目の親を正規分布の標準偏差を決めるために用いる。
- [alpha value (BLX)]
- BLX-α法で用いる両親が作る空間を延長する割合を表す値。
- [mutation method]
- 突然変異の方法を選択。一様分布と正規分布の2種類から選択できる。
- [unified distribution mutation size]
- 一様分布による突然変異を用いる場合の分布幅を定める。但しこの大きさは変数が取りうる値を[-1:1]に正規化したときの大きさに相当する。
- [gaussian distribution mutation SD]
- 正規分布による突然変異を用いる場合の標準偏差を定める。但しこの大きさは変数が取りうる値を[-1:1]に正規化したときの大きさに相当する。
|