- ロンドンへの爆撃
- ギャンブラーの誤謬(公平なサイコロを10回振ったとき、1111111111と5462534351のどちらがでやすいか?)
- 落雷の確率
これについて、代表性ヒューリスティック や少数の法則 というキーワードをもとにして説明して考察せよ。
さらに、ポアソン分布の偏りの錯誤の実例と思われる事象を探し出してみよ。
詳細については この文献とその参考文献などに詳しい。
できるだけ説得力のあるユニークで面白い考察を提出するとポイントが高い。 内容が薄いものは採点しない。
以下のデータや証左をもとにして、比較・検証を詳細に行うこと。
- (WWWや本からの)実測値データ
- 思考実験
- 理論値(ポアソン分布のときは理論値が求められる)
- 自分の実体験
- シミュレーション実験
Hint: 星座、ヒカリムシのパターンとランダムパターンの比較などをしてみよう。 詳細はこの論文(Stephen Jay Gould:Glow, Big GlowwormのPostscript)に詳しい(日本語版はこの本:がんばれカミナリ竜(下)のなかの17章:「光れ、大きなヒカリムシ」の追記にある)。
このページは多くファンがいる。たとえば、 エドワード・ウォーラーとイペット・ベンデックは、13時間足らずでマジックキングダムの全アトラクションを制覇した偉業を達成した。
このHPでは、 待ち行列理論と巡回セールス問題を統合した 手法が使われている。
このHPの技法や実績について説明せよ。
またディズニーランドの以下の戦略はどのくらい有効かについても考察せよ。
- ファストパス:優先入場方式。ばらつきの排除を狙う効果があるが、抜かされた人の不満は増大する。
- 予想待ち時間の看板は実際の待ち時間よりわざと長く表示する手法:控えめに約束して大きな結果を出すサービス戦略
実体験や実測値データなどをもとに解説するとポイントが高い。
Hint: Bob Sehlinger氏の Unofficial Guide to Disneyland Paris などのガイドブックの TOURING PLAN--OF UTMOST IMPORTANCEの記述が参考になる。
このことを以下のように設定を変えて実験してみる。
- J,Q,Kにそれぞれ11, 12, 13の値を割り当てるとき
- J,Q,Kにそれぞれ10の値を割り当てるとき
- J,Q,Kにそれぞれ5の値を割り当てるとき
一致する確率の計算には、ランダムにnの値を2つ選び、「最終カード」が同じになる 確率を求める。
最終カードが一致する確率の理論値はマルコフ過程を用いて 導出することができる。 マルコフ過程を用いたKruskalカウントの解説や理論的考察は 参考書 の3.2節に詳細が記述されている。
| 条件1:JQK=11,12,13 | 条件2:JQK=10 | 条件3:JQK=5 | |
|---|---|---|---|
| 実測値 | 68.2 | 71.2 | 84.2 |
| 理論値( 文献1) | 65.8 | 70.8 | 83.9 |
| 理論値( 文献2) | 65.9 | 71.2 | 70.8 |
文献2 では、すべてのカードは1 からm の値を等しい確率で取ることを仮定したときの 確率推移行列Mが以下のように与えられることから理論値を求めている。
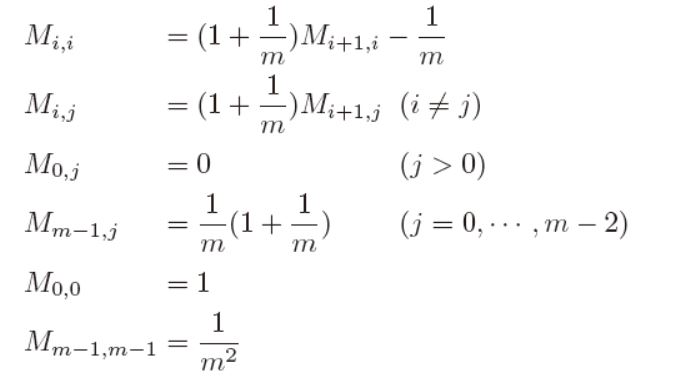
条件2, 3 では,「すべてのカードは1 からm の 値を等しい確率で取る」という制約が破られているため理論値は実測値と一致しない。したがって,より正確な評価には推移確率行列を修正する必要がある。
レポートでは、 より正確に理論値を求める方法(マルコフ過程を用いた方法) を導出し、 条件2, 3の理論値と実測値の比較を行え。
なおKruskalカウントを行うシミュレーションプログラムが ここ にあるので必要なら利用してもよい(Fisher-Yates シャッフルを利用していることに注意)。
- 賭け1: 50%の確率で100ドルを失うが、50%の確率で200ドルをもらえる
- 賭け2: 50%の確率で200ドルを失うが、50%の確率で2万ドルをもらえる
多くの人は、賭け1には手を出さない。 ところが、古典的効用理論に従うと、賭け1を断る人は、賭け2も断ることが証明される。
しかし、当然そんなはずはない。正気の人間なら、賭け2を断ることはないだろう。
このような不合理な結論を伝統的な効用理論が導くことをわかりやすく説明せよ。 レポート作成には この論文などが参考になる。