LGPC for l
LGPCによるBoolean problem(ブール関数問題)を解法するシミュレータです
これは代表的なNP完全問題です。
Problem Configuration
Boolean Function 問題の設定をします。
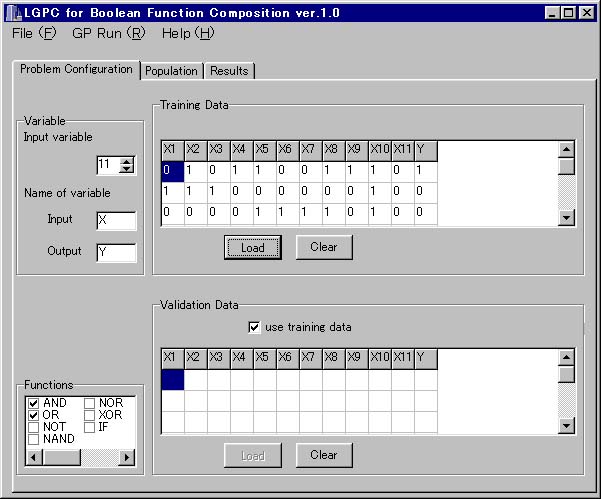
- Variable
Input variable で入力数を 1 〜 16 の範囲で設定します。また、Input, Output でそれぞれ入出力名を入力します。
- Functions
GP の非終端記号としてどの関数を使用するかを選びます。使用したい関数にチェックを入れます。
- Training Data
訓練データの入力を行います。任意のデータを与えることが可能です。ファイルを読み込む場合には Load を押して任意のファイルをロードすることができます。ファイルのサンプルは解凍した Boolean フォルダにあります。また、Clear を押すと入力欄にあるデータをクリアすることができます。
- Validation Data
テストデータの入力を行います。このデータへの適合度により Boolean Function を進化させていきます。use training data をチェックすることで、訓練データをそのまま使うことも可能です。Load, Clear の機能については Training Data と同様です。
Populations
GP におけるパラメータの設定をします。
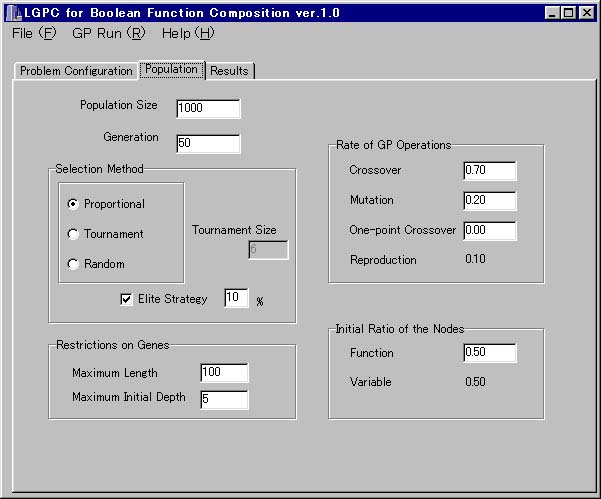
- Population Size
進化させる個体数を設定します。
- Generation
進化させる世代数を設定します。
- Selection Method
次の世代に生き残らせる個体を選択する戦略を決定します。戦略はルーレット方式 (Proportional) 、トーナメント方式 (Tournament) 、ランダム (Random) から選択し、Elite Strategy でエリート戦略を併用するかを選択することもできます。また、トーナメント方式では Tournament Size を、エリート戦略ではその割合を設定することが可能です。
- Restriction on Genes
Maximum Length で進化させる個体の遺伝子の長さの最大値、つまりここでは関数の長さの最大値を設定し、Maximum Inisial Depth でグラフ構造の深さの最大値を設定します。
- Rate of GP Operations
遺伝子の配列が組換え操作されるときの、交叉 (Crossover) 、突然変異 (Mutation)、一点交叉 (One-point Crossover)、そのまま複写 (Reproduction) の遺伝子操作の行われる割合を設定します。
- Initial Ratio of Nodes
グラフ構造においての関数記号 (Function) と 定数 (Variable) の割合を設定します。
Results
シミュレーション結果をリアルタイムで表示します。
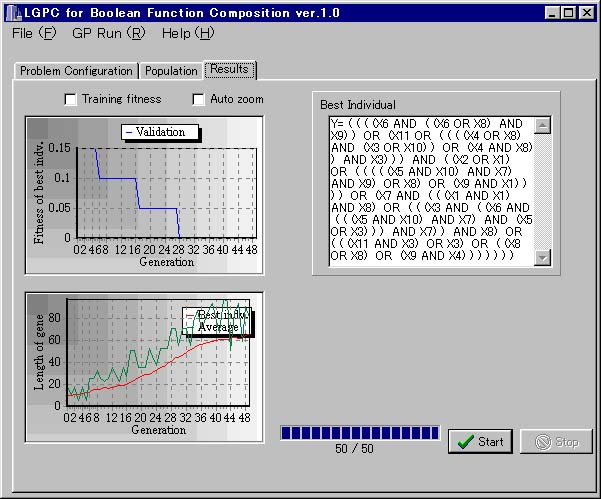
- Fitness of best indv.
各個体を Validation Data と比較したときに、最も適合度の高い個体の適合度を示しています(青線で表示)。Training fitness にチェックを入れることで Training Data との比較も同時に行えます(赤線で表示)。適合度は入力したデータに対しての個体の適合していない割合で表され、0 になったとき完全に入力したデータを満たすことに、つまり、解が求まったことになります。また、Auto zoom で自動的にズームを行うかを設定できます。
- Length of gene
個体の遺伝子の配列の長さ、つまり数式の長さを示しています。赤線が最も適合度の高い個体の数式の長さ。緑線が全個体の平均の長さです。
- Best Individual
最も適合度の高い個体の数式が表示されます。
シミュレーション例と結果
この LGPC for Boolean Function Composition を使ったシミュレーションの一例として、マルチプレクサのチェックパリティの論理式を求めるといったような、付属の 11multi.txt の 11 入力、1 出力のデータを入力、問題設定を行い、各設定のパラメータを変化させてシミュレートしてみました。動作環境は OS : Windows 2000, CPU : PentiumIII 700MHz, メモリ : 384MB です。
11multi.txt では入力 (X) と出力 (Y) の関係が以下のようになっています。
|
|
まず、上述の設定及び使用法のところの図にあるような以下のデフォルトの設定で、シミュレーションを 200 回行いました。また、Validation Data は Training Data と同じデータを使用しました。
Function : AND + OR
Population Size 1000, Generation 50
Selection Method : Proportional + Elite Strategy 10%
Restriction on Genes : Maximum Length 100, Maxmum Initial Depth 5
Rate of GP Operations : Crossover 0.70, Mutation 0.20, One-point Crossover 0.00, Reproduction 0.10
Initial Ratio of the Nodes : Function 0.50, Variable 0.50
結果は以下のようになり、50 世代までで解が求まったのは 62 / 200 = 31% でした。ただし、結果の表中、数字のところは 0 世代目から数えて何世代目で解に到達したかを、×のところは解に到達しなかったことを意味しています。また、解の中で最も短い式も以下のようになりました。以下、この結果を基準に各パラメータを変化させたときのシミュレーション結果の考察をします。以下のシミュレーションでは各 20 回づつシミュレートしました。結果の表記は以下同様です。
Defalt 31%
| × | 42 | × | × | × | × | 35 | × | × | × | × | × | × | × | × | 31 | × | 26 | 37 | 47 |
| × | 30 | × | 16 | × | 28 | 37 | × | × | × | × | × | 34 | × | × | 25 | × | × | × | × |
| × | × | × | × | × | × | × | 37 | 44 | × | × | × | × | × | × | × | 35 | × | × | × |
| 33 | 44 | × | × | 31 | 24 | × | × | × | × | 18 | × | × | × | × | × | × | × | × | × |
| × | × | 48 | × | × | 38 | × | × | × | × | × | × | 23 | × | 16 | × | 25 | × | × | × |
| × | × | 34 | 48 | × | 25 | × | × | × | × | × | × | × | 38 | 27 | × | × | 27 | × | × |
| × | × | 46 | × | 32 | 25 | × | × | 41 | × | × | 23 | × | × | 40 | × | 33 | 46 | × | 43 |
| × | × | 24 | 36 | 46 | × | × | × | × | × | 25 | 24 | × | × | × | × | 36 | × | × | 37 |
| × | × | 28 | 48 | × | × | 32 | × | 22 | × | × | × | 26 | × | × | × | 29 | × | 29 | 26 |
| 29 | × | × | 34 | × | 32 | × | × | × | × | × | × | 32 | × | × | 31 | × | 28 | × | 33 |
Y= ( (X5 AND ( ( (X11 OR ( (X8 OR X11) OR X9) ) AND (X4 OR X1) ) AND X10) ) OR ( ( ( (X2 AND X9) AND (X9 AND (X2 OR (X10 OR (X9 AND X4) ) ) ) ) OR ( ( ( ( (X7 AND X2) OR X7) AND ( ( (X4 AND (X4 OR X1) ) AND (X10 AND X8) ) AND ( (X2 AND (X10 AND X8) ) OR X6) ) ) OR X11) OR (X3 AND X9) ) ) OR X5) )
Functions
使用できる関数を AND + OR から変化させてシミュレートしてみました。各結果は以下の通りです。
AND : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
OR : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
NOT : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
NAND : 20%
| × | × | × | × | × | × | 12 | × | × | × | 17 | × | × | × | × | × | × | × | 43 | 12 |
NOR : 15%
| × | 23 | 35 | × | × | × | × | × | × | 37 | × | × | × | × | × | × | × | × | × | × |
XOR : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
IF : 80%
| 15 | 19 | × | 29 | 12 | × | 24 | × | 26 | 21 | 14 | 32 | 19 | × | 16 | 33 | 15 | 16 | 15 | 11 |
AND + OR + NOT : 40%
| 22 | × | × | × | 35 | 35 | 48 | 24 | × | × | × | 33 | × | 39 | 28 | × | × | × | × | × |
NAND + NOR : 15%
| × | × | × | × | × | × | 21 | × | × | × | × | 16 | 13 | × | × | × | × | × | × | × |
ALL (AND + OR + NOT + NAND + NOR + XOR + IF) : 30%
| 35 | × | 21 | 37 | × | × | × | 21 | 44 | 37 | × | × | × | × | × | × | × | × | × | × |
それぞれ使用する関数によって解の求め易さの違いが見て取れる。さらに、複数の関数を使用するときもそれぞれの解への到達のし易さが反映されている。また、与えられた仮定(入力)によっては解へ到達することができないものがあることがわかる。
Population
進化させる個体数を 1000 から 5000, 200 と変化させて、それぞれシミュレートしてみました。各結果は以下の通りです。
Population 5000 : 50%
| × | 20 | 21 | × | 30 | 39 | × | 26 | × | × | × | 17 | 21 | 32 | × | × | × | 35 | 25 | × |
Population 200 : 10%
| × | 15 | × | × | × | × | × | × | × | 47 | × | × | × | × | × | × | × | × | × | × |
進化させる個体数を増やすと解に到達する確率が高くなり、減らすと確率が下がっていることが確認できる。
Generation
進化させる世代数を 50 から 1000 に変化させてシミュレートしてみました。結果は以下の通りです。
Generation 1000 : 65%
| 93 | 16 | 102 | × | 25 | 28 | 30 | 44 | × | 49 | 316 | 233 | × | 243 | × | 667 | × | × | × | 684 |
進化させる世代数を増やすと、当然、解に到達する確率が高くなる。しかし、世代数が大きくなるに連れて解に到達する確率は低くなっていることがわかる。
Selection Method
生き残り戦略の方法を Proportional から Tournament, Random と変化させて、それぞれシミュレートしてみました。各結果は以下の通りです。また、Tournament の場合 Tournament Size も 6, 30 と 2 通りでそれぞれシミュレートしてみました。各結果は以下の通りです。
Tournament (Tournament Size 6) : 30%
| × | × | 15 | × | 9 | × | × | × | × | × | × | × | × | 7 | 23 | × | 11 | 33 | × | × |
Tournament (Tournament Size 30) : 40%
| × | × | 4 | 25 | 11 | × | × | 34 | × | 11 | × | 6 | × | × | × | × | 9 | × | 6 | × |
Random : 20%
| 38 | × | × | 12 | × | 26 | × | × | × | × | × | × | × | × | × | × | × | × | 41 | × |
また、生き残り戦略の方法は Proportional のままで、Elite Strategy の値を 10% から 0%, 50% と変化させた場合も、それぞれシミュレートしてみました。各結果は以下の通りです。
Elite Strategy 0% : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
Elite Strategy 50% : 20%
| × | 13 | × | × | × | × | × | × | × | × | × | × | × | 43 | × | × | 33 | × | × | 45 |
各戦略の手法による解への到達確率に大差は見られないが、Tournament の場合、トーナメントの大きさが大きくなると解への到達率が高くなっている。また、Elite Strategy は 0% にしてしまうと解へ到達する確率が極めて低くなってしまい、50% と大きくした場合にも、良い結果が得られるわけではない。この値は適度に調節することで、良い結果を導くことになるのではないかと思われる。
Restrictions on Genes
個体の持つ遺伝子の最大長を 100 から 500, 50 と変化させた場合と、遺伝子のグラフ構造の深さを 5 から 25, 1 と変化させた場合についてそれぞれシミュレートしてみました。各結果は以下の通りです。また、遺伝子の最大長 Maximum Length の値を 20 とすると完全にフリーズしてしまいました。バグではないかと思われます。
Maximum Length 500 : 35%
| 38 | × | 35 | × | × | × | × | × | × | × | 28 | 15 | × | × | 24 | × | × | 43 | 33 | × |
Maximum Length 50 : 30%
| × | × | × | 26 | × | 10 | × | × | × | × | × | × | × | × | × | 38 | 34 | 42 | 45 | × |
Maximum Initial Depth 25 : 55%
| × | × | 28 | × | 36 | × | × | 16 | × | 36 | 13 | 41 | × | × | 31 | 24 | 41 | × | 44 | 29 |
Maximum Initial Depth 1 : 30%
| × | × | × | 27 | × | × | 47 | × | × | × | 35 | 22 | × | 48 | × | × | × | 33 | × | × |
遺伝子の長さはこのシミュレーションでは各最大値まで遺伝子の長さが達していなかったため、最大値を大小変化させても影響を与えることなく、変化はなかった。また、グラフ構造を深くすると、探索幅が広くなり解にたどり着く確率が大きくなった。
Rate of GP Operations
遺伝子の配列の組換え操作時の遺伝子操作の割合を (Crossover, Mutation, One-point Crossover, Reproduction) = (0.70, 0.20, 0.00, 0.10) から (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1), (0.25, 0.25, 0.25, 0.25) と変化させてシミュレートしてみました。ただし、(0.25, 0.25, 0.25, 0.25) でのシミュレーションは、良くわからないのですがこのときも完全にフリーズしてしまいました。
(Crossover, Mutation, One-point Crossover, Reproduction) = (1, 0, 0, 0) : 40%
| × | × | × | × | × | 20 | × | 22 | × | 28 | 23 | × | 19 | 32 | × | × | 22 | × | 36 | × |
(Crossover, Mutation, One-point Crossover, Reproduction) = (0, 1, 0, 0) : 15%
| × | × | 27 | × | × | × | × | × | × | × | × | × | × | 32 | × | × | × | × | × | 43 |
(Crossover, Mutation, One-point Crossover, Reproduction) = (0, 0, 1, 0) : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
(Crossover, Mutation, One-point Crossover, Reproduction) = (0, 0, 0, 1) : 0%
| × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × | × |
これらのオペレーションの割合はある1つの種類のオペレーションだけでは進化には有効ではなく、効率よく進化させようとすると、この割合も適当な値にする必要があるようです。
Rate of GP Operations
グラフ構造における関数記号と定数の割合を (Function, Variable) = (0.50, 0.50) から (1, 0), (0, 1) へと変化させてシミュレートしてみました。ただし、(1, 0) のときはフリーズしてしまいました。
(Function, Variable) = (0, 1) : 25%
| × | 43 | 49 | × | × | × | × | 49 | × | × | × | × | × | 40 | 46 | × | × | × | × | × |
