PSOシミュレータ
PSOによる関数最適化のシミュレータです
Particle Swarm Optimization(PSO)とは
このシミュレータはParticle Swarm Optimizationとはどのようなものかを知ろうというソフトです.その概観は以下のとおりです.PSOは1995年にJames Kennedyという人によって提案されたアルゴリズムです.ここでのPSOは3次元空間を数多くの個体が動き回り,それぞれの関数の一番低いところを探すように作られています.それぞれの個体は位置ベクトル,速度ベクトルと,その個体が最良の適合度を獲得した場所だけを記憶しています.そして個体全体の中における最良の適合値の場所の情報もぞれぞれの個体が共有することが出来ます.
すべての個体が世代を経ることにより獲得された最も優れた位置とそれぞれの個体が世代を経ることにより獲得された最も優れた位置の方向へそれぞれの個体が引っ張られると言うと分かりやすいでしょうか.その方法は以下の式によって行われます.
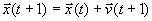
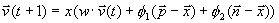
- φ1…0から2までの乱数です.
- φ2…同じく0から2までの乱数です.
- χ…0.9から1.0までの乱数です.
- ω…0.9の固定値.入力のところで変更することは出来ます.
ダウンロード
Particle Swarm Optimization ver1.0 (402KB)
このファイルをダウンロードし解凍すると「EquToDbl.dll」と「EquToDbl.txt」と「PSO.exe」という3つのファイルが出てきます.そして「PSO.exe」をクリックするとPSOを起動することができます.なおこのシミュレータにはやす兵衛さんが作られた数式計算DLLを利用させていただいています.
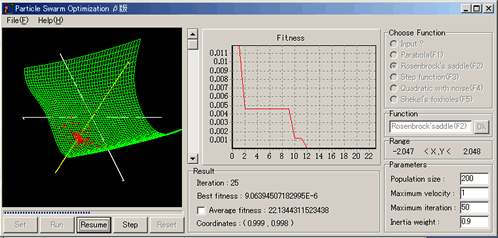
PSO Simulatorの使い方
PSOの遊び方は簡単です.わからないところがあればこの使い方の説明のあとにある各機能の説明についても読んでみてください.
- Setボタン
Setボタン押すと初期集団が生成されます.
- Runボタン
これを押すと計算を始めます.
- Stopボタン
これを押すと計算を中断することができます.途中の個体の動きをじっくり見たいときとかに使ってください.
- Stepボタン
Stopボタンを押したあとStepボタンは使えるようになります.Stepボタンは世代ごとの動きを逐次見ることができます.
- Resetボタン
計算が終わったらこれを押してください.もう一度始めることができます.
Parameter
- Population Size
集団サイズのことです.
- Maximum Verocity
個体が動くときの最大速度です.これ以上速くは動きません.
- Maximum Iteration
反復回数です.
- Inertia Weight
上にある2式のうち下のほうのWの値です.標準では0.9になっています.こうすることによって速度はだんだん弱まっていきます.
Choose Function
- Input?
これにチェックを入れると自由に関数を定義することができます.変数は小文字の xとy です.大文字の XやYは使えません.他に使える関数は以下のとおりです.ただし,これを使うと非常に重くなってしまいます.原因究明中です….
| [定数] |
数値 pi deg e g T0 P0 |
数値定数(1, 2.0, 3.0E10 等) 円周率(3.1416...) pi / 180 自然対数の底(2.7182....) 重力加速度(9.80665) 絶対温度(273.15) 大気圧(101325) |
| [演算子] |
- + - * / ^ ! |
負の数値 四則演算 ベキ乗 階乗 |
| [関数] |
abs(x) |x| sqrt(x) exp(x) log(x) log10(x) sin(x) cos(x) tan(x) asin(x) acos(x) atan(x) sinh(x) cosh(x) tanh(x) |
絶対値 絶対値 平方根 指数 自然対数 常用対数 サイン コサイン タンジェント 逆サイン 逆コサイン 逆タンジェント ハイパボリックサイン ハイパボリックコサイン ハイパボリックタンジェント |
ここから下に書いてある式はDeJongの標準化関数といわれています.F1〜F5まであり,GAのベンチマークテストや他の手法との定量的評価手段として用いられています.その関数は以下のようなものです.
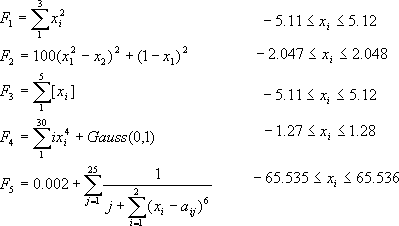
- Parabola(F1)
単峰性の山の形をしているので解くのは簡単.
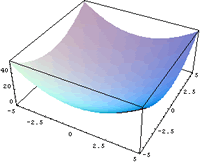
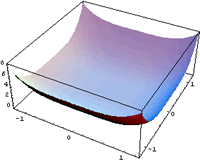
- Rosenbrock's saddle(F2)
これも単峰性の山の形をしているので解くのは簡単.
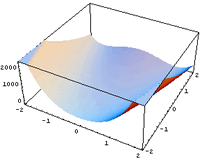
- step function(F3)
これは階段状になっているので少し難しい.
- quadratic with noise(F4)
これはF1にノイズがのったような感じ.一応多峰性関数.すこし難しい.
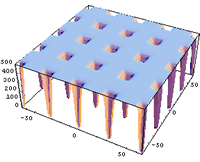
- Shekel's foxholes(F5)
これは難しい.多峰性関数.とんがっているので一度落ちると抜け出るのも大変.特に適合度が2の場所が曲者.刺さると痛い.
Result
- Iteration
ここに表示されるのは反復回数です.世代数といってもいいも知れません.
- Best fitness
それぞれの個体が見つけた一番小さな値です.
- Average fitness
個体全体の適合度の平均です.ここにチェックをいれるとグラフにこの適合度も表示させることが出来ます.しかし,Best fitnessとの差があり過ぎるので出来るだけやめた方がよいです.
- Coordinate
Best fitnessの場所を表しています.
ちなみにGAとの比較
- F2,F5においてGAと比較してみました
このPSOシミュレータとGA3Dシミュレータを用いて比較を行いました.下のグラフは20回の試行の平均値です.ただし,ここでのPSOとGAとの比較には問題があります.厳密な比較は出来ていません.なぜでしょうか?考えてみましょう.
| GA | PSO | |
| 世代数 | 50 | 50 |
| 個体数 | 200 | 200 |
| 交叉率 | 0.7 | |
| 突然変異率 | 0.01 | |
| 遺伝子長 | 13 | |
| エリート戦略 | 5% | |
| 交叉方法 | 一点交叉 | |
| コーディング方法 | バイナリ | |
| 最大速度 | 1 | |
| 慣性の重み | 0.9 |
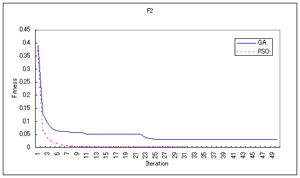
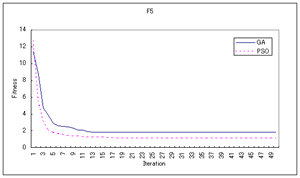
PSOってすごいですね〜〜.
参考文献
さらに詳しく知りたい方は以下の論文などを参考にしてください.とりあえず日本語の本はないです.
- James Kennedy and Russell Eberhart.Particle Swarm Optimization.Proceedings of IEEE the International Conference on Neural Networks,1995
