Abstract
Estimation
of Distribution Algorithms (EDAs) is a new area of Evolutionary Computation. In
EDAs there is neither crossover nor mutation operator. New population is
generated by sampling the probability distribution, which is estimated from a
database containing selected individuals of previous generation. Different approaches
have been proposed for the estimation of probability distribution. In this
paper I provide a review of different EDA approaches and present three
solutions based on Univariate Marginal Distribution Algorithm (UMDA) to
optimization in binary and non-binary search spaces. Three well-known problems:
Subset Sum problem, OneMax function and n-Queen problem are solved and the
experimental results comparing UMDA with or without local heuristics and GAs
are given. From my experiments it seems that UMDA may perform better for linear
problems of without dependencies among variables.
Keywords
Estimation
of Distribution Algorithm, 2-opt local heuristic,
1.
Introduction
Genetic Algorithms (GAs) are
optimization techniques based on selection and recombination of promising
solutions. The collection of candidate solutions is called populations of
Genetic Algorithms whereas candidate solutions are sometimes named as Individuals,
Chromosomes etc. Each Individual is an encoded representation of variables of
the problems at hand. Each component (variable) in an Individual is termed as
Gene. Sometimes the components (genes) are independent of one another and
sometimes they correlated. But always a communication and information exchange
among individuals in a population is maintained through the selection and
recombination operator of Genetic Algorithm. This kind of exchange helps to
combine partial solutions (individuals) to generate high quality partial
solutions-building blocks (BBs) (Holland 1975; Goldberg 1989). The
behavior of the GAs depends on the choice of the genetic operators-selection,
crossover, mutation, probabilities of crossover and mutation, population size,
rate of generational reproduction, number of generations etc. But seldom the
problem specific interactions among the variables are considered. As a result,
the fixed two parents recombination and evolution sometimes provide inferior
quality of solution converging to a local optimum. To avoid the disruptions of
partial solutions, the two parents recombination processes can been replaced by
generating new solutions according to the probability distribution of all
promising solutions of the previous generation. This new approach is called
Estimation of Distribution Algorithm (EDA). EDAs were introduced in the field
of Evolutionary Computation for the first time by Mühlenbein and Paab (1996).
2. Estimation of Distribution Algorithm (EDA)
In EDAs the problem specific interactions among the variables of individuals are taken into consideration. In Evolutionary Computations the interactions are kept implicitly in mind whereas in EDAs the interrelations are expressed explicitly through the joint probability distribution associated with the individuals of variables selected at each generation. The probability distribution is calculated from a database of selected individuals of previous generation. The selections methods used in Genetic Algorithm may be used here. Then sampling this probability distribution generates offspring. Neither crossover nor mutation has been applied in EDAs. But the estimation of the joint probability distribution associated with the database containing the selected individuals is not an easy task. The following is a pseudocode for EDA approach:
Step 1: 
Generate
M individuals (the initial population) at random
Step 2: Repeat steps 3-5 for l=1,
2, … until the stopping criteria met
Step 3: Select N<=M individuals from Dl-1
according to selection method
Step 4: Estimate
the probability distribution of an individual being among the selected
individuals
Step 5: 
Sample M
individuals (the new population) from pl(x)
3.
Different EDA approaches
3.1 Independent Variables
The easiest way to calculate
the estimation of probability distribution is to consider all the variables in
a problem as univariate. Then the joint probability distribution becomes the
product of the marginal probabilities of n variables,
i.e.
.
Univariate Marginal Distribution Algorithm (UMDA) (Mühlenbein, 1998), Population Based Incremental Learning (PBIL) (Baluja, 1994) and Compact Genetic Algorithm (cGA) (Harik et al., 1998) consider no interaction among variables. In UMDAs the joint probability distribution is factorized as a product of independent univariate marginal distribution, which is estimated from marginal frequencies:
if in the jth case of 
, Xi=xi
; =0, otherwise.
In PBILs the population of
individuals is represented by a vector of probabilities: pl(x)=(pl(x1),…,
pl(xi),…,pl(xn)) where pl(xi)
refers to the probability of obtaining a 1 in the ith component of Dl,
the population of individuals in the lth generation. At
each generation M individuals are generated by sampling pl(x)
and the best N individuals are selected. The selected individuals are used to
update the probability vector by a Hebbian inspired rule:
where aÎ(0,1] and 
represents the value of xi
at kth selected individual. The update rules
shifts the vector towards the best of generated individuals.
In CGAs the vector of
probabilities is initialized with probability of each variable 0.5. Then two
individuals are generated randomly by using this vector of probabilities and
rank them by evaluating. Then the probability vector pl(x) is
updated towards the best one. This process of adaptation continues until the
vector of probabilities converges.
All the above mentioned algorithm provides better results for variable with no significant interaction among variables (Mühlenbein, 1998; Harik et al., 1998; Pelikan and Mühlenbein ,1999) but for higher order interaction it cannot provide better results.
3.2 Bivariate Dependencies
To solve the problems of pairwise interaction among variables population based Mutual Information Maximizing Input Clustering (MIMIC) Algorithm (De Bonet et al., 1997), Combining Optimizers with Mutual Information Tress (COMIT) (Baluja and Davies, 1997), Bivariate Marginal Distribution Algorithm (BMDA) (Pelikan and Mühlenbein, 1999) were introduced. Where there is at most two-order dependency among variables these provide better result that is far away from the real world where multiple interactions occur.
3.3 Multiple Dependencies
Factorized Distribution
Algorithm (FDA) (Mühlenbein et al.
1998), Extended Compact Genetic Algorithm (ECGA) (Harik, 1999), Bayesian
Optimization Algorithm(BOA) (Pelikan et al., 2000), Estimation of Bayesian
Network Algorithm (EBNA) (Larraňaga et al., 2000) can capture the multiple
dependencies among variables.
FDA uses a fixed
factorization of the distribution of the uniformly scaled additively decomposed
function to generate new individuals. It efficiently optimizes a class of
binary functions, which are too difficult for traditional GAs. FDA
incrementally computes Boltzmann distributions by using Boltzmann selection.
FDA converges in polynomial time if the search distribution can be formed so
that the number of parameters used is polynomially bounded in n (Mühlenbein
and Mahnig,2002). But the problem of FDA is the requirement of fixed
distribution and additively decomposed function.
BOA uses the techniques from modeling data by Bayesian Networks to estimate the joint probability distributions of selected individuals. Then new population is generated based on this estimation. It uses the BDe(Bayesian Dirichlet equivalence) metric to measure the goodness of each structure. This Bayesian metric has the property that the scores of two structures that reflect the same conditional dependency or independency are the same. In BOA prior information about the problem can be incorporated to enhance the estimation and better convergence (Pelikan et al., 2000). In order to reduce the cardinality of search space BOA imposes restriction on the number of parents a node may have. For the problems where a node may have more than 2 parents, the situation is complicated to solve.
In ECGA the factorization of
the joint probability is calculated as a product of marginal distribution of
variable size. These marginal distributions of variable size are related to the
variables that are contained in the same group and to the probability
distribution associated with them. The grouping is carried out by using a
greedy forward algorithm that obtains a partition among the n variables.
Each group of variables is assumed to be independent of the rest. So the
factorization of the joint probability on n variables is:
where Cl denotes the set of groups
in the lth generation and pl(xc) represents
the marginal distribution of the variables Xc , that is the
variables that belong to the cth group in the lth
generation. ECGA uses model complexity and population complexity to measure the
quality of the marginal distribution. It can cover any number of interactions among variables but the
problem is, it does not consider conditional probabilities which is
insufficient for highly overlapping cases.
In
EBNA the joint probability distribution encoded by a Bayesian Network is learnt
from the database containing the selected individuals in each generation. The
factorization can be written as: 
where 
is the set
of parents of the variable Xi. Different algorithms can be
obtained by varying the structural search method. Two structural search methods
are usually considered: score+search and detecting conditional (in)
dependencies (EBNAPC). Particularly two scores are used in the
score+search approarch: the Bayesian Information Criterion (BIC) score (EBNABIC)
and the 
or by maximum likelihood estimates: 
where Nijk denotes the
number of cases in the selected individuals in which the variable Xi
takes the kth value and its parents Pai
take jth value and 
.For the
case of expected values when the selection is elitist EBNAs converge to a
population that contains the global optimum whereas for maximum likelihood case
it is not guaranteed( González et al.).
4. Univariate Marginal Distribution Algorithm (UMDA)
In UMDA it is assumed that
is there is no interrelation among the variables of the problems. Hence the
n-dimensional joint probability distribution is factorized as a product of n
univariate and independent probability distribution. That is:
.
Each
univariate marginal distribution is estimated from marginal frequencies: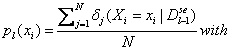 
if in the jth case of , Xi=xi
=0, otherwise.
The pseudocode for UMDA is as follows:
Step-1:D0¬Generate M individuals (the initial population) at
random
Step-2: Repeat steps 3-5 for l=1,2,…
until stopping criteria is met
Step-3: Dl-1¬ Select N£M individuals from Dl-1
according to selection method
Step-4: Estimate the joint probability
distribution
Step-5: Dl¬Sample M individuals (the
new population) from pl(x)
4.1 Convergence of UMDA by Laplace correction
González et al. has shown
that some instances with pl(x)³d>0 visits populations of D*
which contains global optimum infinitely with probability 1 and if
the selection is elitist, then UMDA may converge to a population that contains
the global optimum.
But
the joint probability distribution of UMDA can be zero for some x;
for example, when the selected individuals at the previous steps are such that 
for all j=1, 2, …, N. Hence pl(x)=0.
So UMDA sometimes may not visit a global optimum (González et al.).
To
overcome the problems the way of calculating the probabilities should be
changed. One possible solution is to apply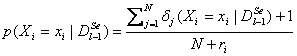 
where ri is the number of
different values that variable Xi may take.
5. Some Solutions by UMDA
Here I have applied Univariate Marginal Distribution Algorithm to some well-known problems like Subset Sum problem, n-Queen Problem and OneMax function with some local heuristics.
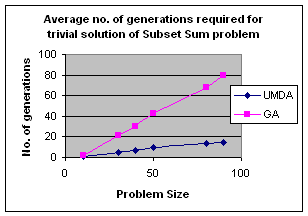
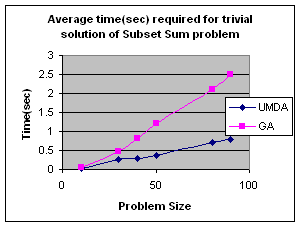
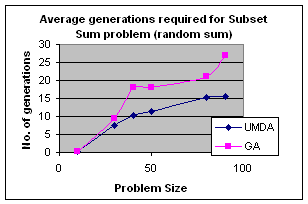
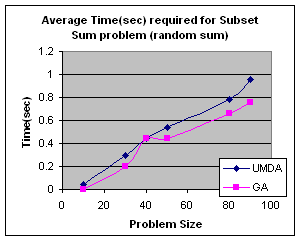
5.1 Subset Sum Problem
It is the problem of finding what subset of a list of integers has a given sum. The subset sum is an integer relation problem where the relation coefficients are either 0 or 1.If there are n integers, the solution space is 2n which is the number of subsets for n variables. For small n exact solutions can be found by backtracking method but for larger n state space tree grows exponentially. It is an NP-Complete problem.
5.1.1 Solving Subset Sum Problem with UMDA
In UMDA each individual
(solution) is represented by an n-tuple (x1,x2,x3,…xn)
such that xiÎ{0,1}, 1£i£n. Then xi=0
if ith integer is not selected and xi=1 if
selected. Each individual is evaluated by finding the difference between the
expected sum and the sum of the selected integers in the individual. The
smaller difference is the better. Marginal probability distribution is
calculated from the best half of the solution with
5.1.2 Genetic Algorithm for Subset Sum Problem
Using same representation, initialization, evaluation and replacement strategy as UMDA I apply GA to the problem. I use simple one point crossover and mutation for generation of offspring. Parents have been selected randomly for crossover.
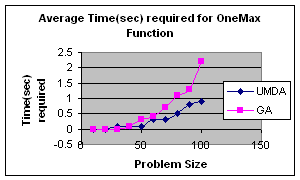
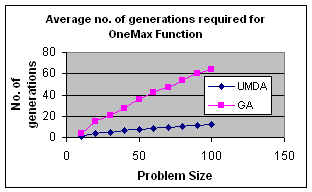
5.2 OneMax by UMDA
OneMax
function returns the number of ones in an input string, i.e.,
where X={X1,X2,…,Xn}
and XiÎ{0,1}
It is a unimodal function which has optimum in XOpt={1,1,…,1}.It is a trivial function which is used as a test function for the evaluation of performance of Genetic Algorithms and
EDAs.
With
In my experiment I initialize population randomly, selected best half for calculation of probability distribution and elitism for replacement. The result is satisfactory.
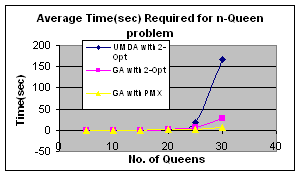
5.3 n-Queen Problem
n-queen problem is a classic combinatorial problem. The task is to place n-queen on an n´n chessboard so that no two queens attack each other; that is, no two queens are on the same row, column, or diagonal. Let us number the rows and columns of the chessboard 1 through N and so the queens. Since each queen must be placed on a different row, we can assume that queen i is to be placed on row i.
Let the solution be X={X1, X2,…, Xn} where Xi represents the column position in row i where queen i can be placed. As all queens must be on different columns, all Xi s must be different. So the solution will be a permutation of the numbers 1 through n and the solution space is drastically reduced to n!.
We can easily fulfill the first two constraints-no two queens on the same row or column by allowing distinct value for each Xi. But how to test whether two queens at positions (i,j) and (k,l)[i=row,j=column] are on the same diagonal or not? We can test it by some observations:
Every element on the same diagonal that runs from upper left to lower right has the same row and column value [(i,i) form] or same (row-column) value.
Every element on the same diagonal that goes from the upper right to the lower left has same row+column value
So two queens are on the same diagonal if i-j=k-l or i+j=k+l.
These
two equations can be rewritten as j-l=i-k and j-l=k-i.
That is, if abs(j-l)=abs(i-k) then the two queens are on the same diagonal.
So the pseudocode for the testing of the constraints for the queens at position Xi and Xj is:
If ((Xi=Xj) OR (abs(i-j)=abs(Xi-Xj)) then
return NOT_FEASIBLE;
But this algorithm requires (n(n-1)/2) comparisons to calculate the fitness of an individual.
5.3.1 Solving n-Queen using UMDA
With UMDA the individual in a population is represented as {X1,X2,…,Xn} where each Xi represents the column at row i where ith queen is placed. The fitness of individual is calculated as the number of queens at non-attacking positions.
The initial population of size M is generated randomly with constraints that all values in an individual are distinct numbers of the set {1, 2,…,n}.By doing this I have implicitly satisfied the constraints that no two queens are on the same row or column. Then, fitness calculation is just to check whether two queens are on the same diagonal or not.
In
each generation the best half of the individuals of the previous generation are
selected for the calculation of joint probability distribution using marginal
frequency of each Xi. During calculation of marginal
distribution of each variable
Then
M new individuals are generated. During generation of each individual I
have applied probabilistic modification to enforce the first constraint
of n-Queen. In probabilistic modification when some variables are selected
their probabilities for the next turn have been zero and the probability of non
selected variables are increased proportionately. Consider the following
example:
|
Before Selection of X1 |
|
After Selection of X1 |
|||||
|
Position/ Variable |
1 |
2 |
3 |
|
1 |
2 |
3 |
|
X1 |
0.7 |
0.1 |
0.5 |
|
0.7 |
0 |
0 |
|
X2 |
0.1 |
0.6 |
0.1 |
|
0.1 |
0.65 |
0.35 |
|
X3 |
0.2 |
0.3 |
0.4 |
|
01. |
0.35 |
0.65 |
Table 1: Probabilistic modification example
If X1 is selected for first position then the probability of X1 for 2nd and 3rd position should be zero and the probabilities of X2 and X3 will increase proportionally. The temporary table should look like the one at the right above. By doing this we can ensure that distinct value will be generated for each component of an individual if Roulette Wheel selection is used.
For replacement strategy I have use elitism The algorithm stops when fitness of the best individual is n; that is, all queens are at non-attacking position or certain number of generations have passed.
Fitness improvement heuristics can be applied to the problem and performs much better than blind search using UMDA. For combinatorial optimization 2-opt (Croes, 1992) algorithm or Partially Matched Crossover (PMX) (Goldberg et al., 1987) is widely used. I have used 2-opt algorithm. The resulting algorithm is:
Figure
1. Algorithm for solution of n-Queen problem by UMDA with 2-opt local heuristic
