GPのイメージ
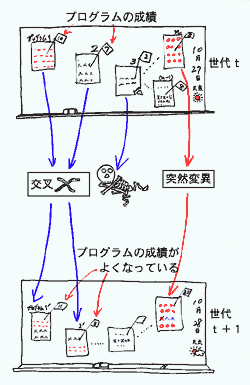
遺伝的プログラミング(GP)は、遺伝的アルゴリズム(GA)の遺伝子型を構造的な表現が扱えるように拡張し、プログラム生成や学習、推論、概念形成などに応用することを目指しています。GPの考え方をAIに適用し、学習、推論、問題解決を実現する試みを進化論的学習と呼びます。右図にGPのイメージを示します。
GPの基本
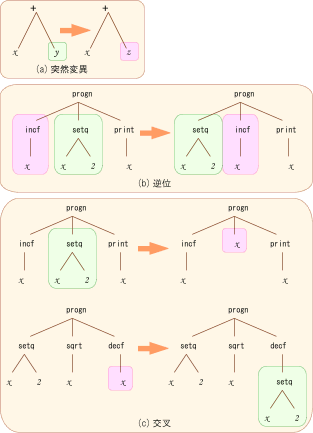
GPでは、グラフ構造(特に木構造)を扱えるようにGAの手法を拡張します。一般的に木構造はLISPのS式 で記述できるので、GPでは遺伝子型としてLISPのプログラムを扱うことが多いです。さらに木構造に対する GPオペレータとして次のようなものを用意します。
- 突然変異 … 部分木の変更
- 逆位 … 兄弟木の並び替え
- 交叉 … 部分木の取り替え
後はGAと同様に、選択淘汰、生殖を繰り返します。そうすれば、図のオペレータにより少しずつプログラムの構造が変化し、より適した(賢い)プログラムが残っていき、最終的に目的の(最適な)プログラムが探索 できるというわけです。また、図2木構造で、下に枝があるノード(節)を非終端記号(関数記号)といい(+、progn、incfなど)、一方、下に枝をもたないノードを終端記号をいいます(定数、変数など)。
Linear GPとは
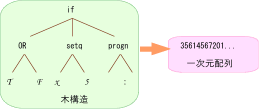
上述のGPでは、遺伝子型として木構造のプログラムを扱っていますが、Linear GP では遺伝子型として1次元配列を扱います。つまり、GTYPE(遺伝子型)を1次元配列とし、木構造のプログラムをこの1次元配列であらわします。オペレータは木構造を操作するのではなく、1次元配列を操作することになります。これにより、ポインタ参照のオーバーヘッドを激減し、高速かつ、メモリ消費の小さいシステムになります。従来のポインタ形式のシステムに比べ、1/4から1/2の実行時間で同等以上の計算ができ、またメモリ消費量は1/4以下に低減できます。
問題は、「如何にして木構造のプログラムを1次元配列にコーディングするか」ですが、これはスタックカウンタの考え方をもちいて解決できます。詳しくは以下の論文を参照してください。
- "Empirical and Statistical Analysis of Genetic Programming with Linear Genome," in Proc. 1999 IEEE International Conference on Systems, Man and Cybernetics (SMC99), , IEEE Press, 1999
- 伊庭斉志,"遺伝的プログラミングと進化論的計算手法",人工知能学会誌,Vol.15,no.2,2000
GPの応用例
ここではGPの応用例として、REGRESION問題とANT問題を紹介します。REGRESION問題とANT問題は LGPCで実際に解いてみることができます。ともに、訓練データで学習し、学習したものをテストデータでテストできます。
REGRESION問題
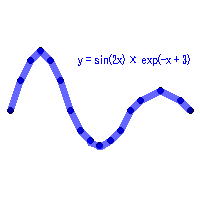
REGRESION問題とは、ある関数(データ系列)を、適当な演算子や関数、定数を用いて同定(近似)しよう というものです。例えば、sin(x) を、+、−、×、÷と、0から100までの実数で近似せよ、という問題です。 実際には、ある実験結果のデータ系列から、その理論式を同定するときなどに使います。

ANT問題
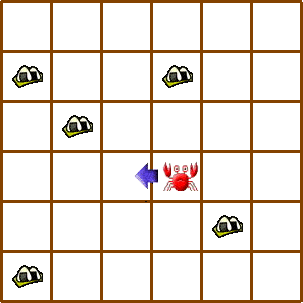
ANT問題とは、人工蟻がある時間内で、餌を探索するというものです。例えばLGPCでは、図5のように餌 は碁盤目上にばらまかれており、人工蟻はある決められたエネルギーを持っています。人工蟻は、一歩前 に進むか方向を変えるたびに、エネルギーをひとつずつ失っていきます。そして、エネルギーが0になるまで に、できるだけ多くの餌を見つけるようなプログラムを探します。
私たちの研究室では
私たちの研究室では、遺伝的プログラミングを用いたマルチエージェント学習、システム同程問題の解法、株式データ(日経平均株価)の予測、ロボットプログラム、並列実装、高速な遺伝的プログラミングシステムの構築(linear GP) などを研究しています。